Ich hatte mal einen Kollegen, der während der Arbeitszeit immer an der Börse gezockt hat, meist nebenher auf dem Handy - Aktien, KO-Scheine oder CFDs, alles Dinge, mit denen er Geld verlieren würde.
Ich versuchte es ihm zu erklären und auszureden, aber er verstand es nicht, oder er wollte es nicht verstehen, oder er glaubte mir nicht. Darum beschloß ich damals, ein Programm zu schreiben, einen Börsensimulator, mit dem ich es demonstrieren könnte.
Gesehen hat mein Kollege das Programm nie. Dazu kam es nicht mehr, weil ich den Arbeitgeber wechselte und er auch. Ich weiß gar nicht mehr, wer zuerst ging.
Das Programm hatte ich liegen lassen. Andere Dinge waren wichtiger. Mir hatte es gezeigt, was ich zeigen wollte. Ich sah keinen Bedarf, es weiter- oder fertig zu entwickeln, und es wäre wohl bis heute so geblieben, wenn ein Kumpel mir nicht neulich gesagt hätte, daß er jetzt auch ins Business eingestiegen sei, er handele mit EUR/USD, Forex, Hebel, habe einen Bot programmiert. Der Reichtum sei zum Greifen nahe.
Ich verwies auf mein Programm, auf OpenSeSim - den Open Source Stock Exchange Simulator, womit mein Kumpel vielleicht der erste neben mir war, der damit einmal rumgespielt hat - und vielleicht noch der Typ, der dem Projekt auf Github irgendwann einen Stern gegeben hat.
Meinen Kumpel hat das Programm allerdings (noch) nicht überzeugt. Er wird erst mal weiter machen mit Forex, Hebel und Metatrader, bis sein Geld alle ist, vielleicht noch mal nachschießen, dann nochmal und nochmal, wer weiß das schon.
Derweil hab ich OpenSeSim aus seinem nunmehr fast neun Jahre währendem Dornröschenschlaf auf Github erweckt, das ganze etwas aufgeputzt, Features vervollständigt, Bugs beseitigt, womit ich die Software nun doch einmal vorstellen möchte.
Da ich an die Gültigkeit der Markteffizienzhypothese glaube und damit Kursbewegungen einem Random Walk gleichen müssen, halte ich es für unsinnig, Handelssysteme und Trading-Bots an historischen Kursen zu backtesten, denn du selbst bist der Kurs, du bist Teil des Systems.
Was bringt es, ein System für eine in der Vergangenheit zufällig gewürfelte Zahlenfolge zu optimieren? Erwartest du ernsthaft, daß es für zukünftige Zufallsfolgen dann auch optimiert ist? Warum würfelst du die zukünftigen Zufallszahlen nicht gleich selbst aus?
Mit OpenSeSim wollte ich eine einfache Möglichkeit schaffen, mit Trading-Bots herumzuspielen, und zwar mit Trading-Bots, die nicht auf historischen Kursen handeln, sondern mit sich selbst gegeneinander und damit die Kurse bilden - eine Börsensimulation eben.
Die größte Hürde für den Nutzer ist vielleicht die Installation von OpenSeSim. Hier kannst du das Programm herunterladen und findest eine Anleitung zur Installation.
OpenSeSim ist in Java geschrieben (Aufschrei: Was?) und verwendet Swing (Was? Das gibts noch? Schrei von Munch!), aber das Schöne an Swing ist, daß du dir damit das Look and Feel von CDE/Motiv einstellen kannst (der Saal leert sich, nur die wirklich Interessierten sind noch da).
Wenn du also noch dabei bist, nach der Installation OpenSeSim zum ersten Mal startest und den Run-Knopf drückst, erhältst du nach kurzer Zeit (Acceleration auf 1000x oder höher setzen!) einen Chart etwa wie diesen:
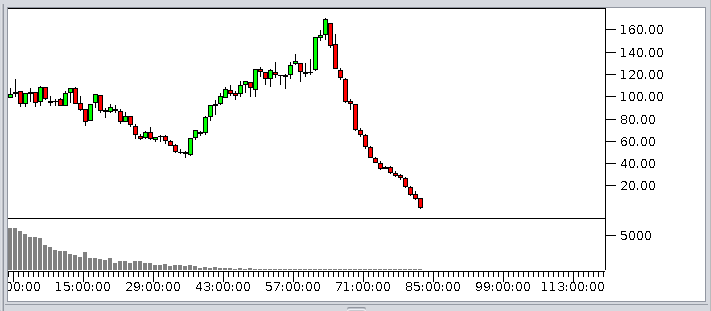
Was ist da passiert?
Alice gegen Bob
In der Standardkonfiguration von OpenSeSim gibt es zwei Trader, Alice und Bob, die im klassischen Aktienhandel gegeneinander antreten. Sie handeln also ohne Hebel und ohne Margin, sie handeln nur Long.
Bob besitzt zu Beginn 10.000 Euro und 100 Aktien, Alice startet mit einer Million Euro und 10.000 Aktien. Beide handeln nach dem selben System: Sie positionieren zufällig zwischen -2% und +2% vom aktuellen Kurs eine limitierte Kauf- oder Verkaufsorder, und wenn die Order ausgeführt wurde, beginnen sie das Spiel von vorn. (Auch, wenn die Order nach einer gewissen Zeit keinen Fill bekommt, versuchen sie es erneut mit einem zufälligen Limit).
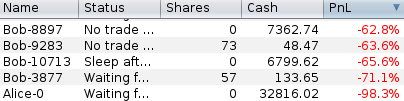
Das Ergebnis: Bob ist nach kurzer Zeit pleite. Alice hat Bobs Aktien und auch sein Geld.

Du kannst die Simulation beliebig oft wiederholen (Stop-Knopf drücken, Run-Knopf drücken), Bob geht immer pleite, Bob ist immer der Verlierer.
Weil Bob weniger Geld als Alice hat, krepiert er am Gamblers Ruin.
Der Gamblers Ruin wird gern mit einem einfachen Münzwurfspiel veranschaulicht: Alice und Bob werfen eine faire Münze, wenn Alice gewinnt, muß Bob einen Euro an Alice zahlen, gewinnt dagegen Bob, erhält er einen Euro von Alice. Obwohl bei dem Spiel für beide die Gewinnchancen identisch sind, es also langfristig keinen Gewinner gibt, ist Bob der Loser, denn, da Alice deutlich mehr Geld hat, ist sie imstande, größere Verluste auszuhalten. Nehmen wir an, Bob hat 1000 Euro und Alice eine Million, dann muß Bob nur 1000 Spiele mehr verlieren als er gewinnt, was auf lange Sicht sicher einmal passiert, und schon ist er pleite. Bei Alice dagegen muß die Differenz aus verlorenen und gewonnen Spielen eine Million betragen, damit sie pleite ist.
Aber was hat das mit dem Zocken an der Börse zu tun?
Hier verhält es sich so: Wenn Alice ein Limit-Order plaziert, bietet sie ihren gesamten Aktienbestand zum Kauf an oder versucht für sämtliches Geld, das sie hat, Aktien zu kaufen. Der arme Bob kann Alice aber immer nur einen kleinen Teil ihrer Aktien abkaufen. Dadurch setzt Alice mit jedem Trade nur einen Bruchteil ihres Vermögens aufs Spiel (der eine Euro aus dem Münzwurfspiel), während Bob immer full-in geht (Bob hat im Prinzip nur einen Euro). Auch, wenn Bob kleinere Positionsgrößen verwendet, zum Beispiel immer nur 10%, geht er pleite - es dauert nur länger.
Alice gegen viele Bobs
Aber was passiert, wenn Alice gegen mehr als einen Bob antritt?
Du kannst es ausprobieren! Laß mit OpenSeSim 100 Bobs mit jeweils 10.000 Euro und 100 Aktien gegen eine Alice mit einer Million Euro und 10.000 Aktien antreten. (Edit -> Traders, dort die Zahl der Bobs auf 100 erhöhen)
Das Ergebnis ist genauso traurig wie vorher. Alle Bobs sind pleite, Alice besitzt sämtliche Aktien, die die Bobs zu Beginn hatten, und deren Geld hat sie auch.
Verrückt, oder? Hättest du das erwartet?
Doch wie sieht es aus mit 1000 Bobs gegen eine Alice? Auch nicht besser. Alle Bobs gehen pleite. Und 5000 Bobs gegen Alice? Nope! Auch hier gehen alle Bobs pleite und Alice bekommt deren Geld und deren Aktien.
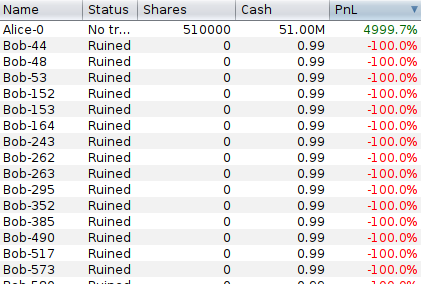
Die Reichen werden immer reicher, und die Armen immer ärmer. Im realen Leben würden die Bobs, nachdem sie pleite sind, arbeiten gehen, um ihr Tradingkonto wieder aufzufüllen. Das Geld für ihre Arbeit bekommen sie von Alice, und mit ihrer Arbeit bauen die Bobs Paläste, Yachten und rote Sportautos für Alice - all das, was die Bobs selbst gern hätten.
Ja, haben denn die Bobs überhaupt irgendeine Chance, gegen Alice zu gewinnen?
Klar!
Der Super-Bob
Die Ursache, daß Alice auch gegen viele Bobs gewinnt, selbst, wenn die Bobs zusammen deutlich mehr Geld und Aktien als Alice haben (5000 Bobs haben zusammen immerhin 50 Millionen Euro und 500.000 Aktien), liegt darin, daß Alice mit ihrer zum einzelnen Bob verglichenen größeren Geldmenge mehr Marktmacht hat, was meint, daß sie mit ihren großen Orders den Kurs in die eine oder andere Richtung leicht bewegen kann. Dies gibt ihr beim Münzwurfspiel einen kleinen Vorteil, der sich ausweitet, je mehr Geld sie bekommt. Daher sehen wir zu Beginn einer Simulation von Alice gegen 5000 Bobs, daß der Kurs scheinbar mehr oder weniger seitwärts läuft, aber zum Ende hin, wenn Alice reicher und reicher geworden ist und vor allem die Bobs ärmer geworden sind und kaum noch nennenswerte Stückzahlen an Aktien kaufen können, der Kurs immer heftigere Kapriolen schlägt, was schließlich die letzten Bobs ruiniert.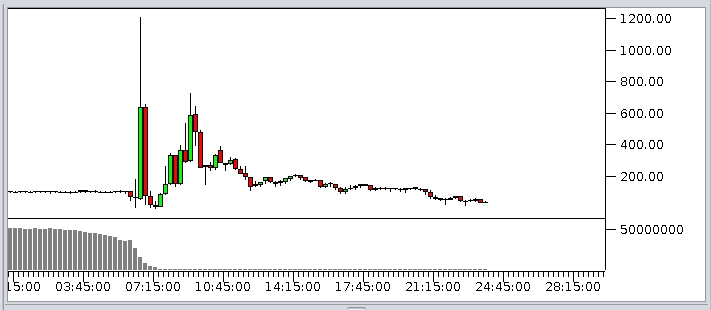
Was können die Bobs also tun, um Alice zu besiegen? Ganz einfach! Sie müssen sich zusammenrotten und konzertiert ihre Orders zur selben Zeit an dieselbe Stelle ins Orderbuch setzen. Gemeinsam sind sie stark, eine Big Alice, sie sind der Super-Bob.
In OpenSeSim würden wir das simulieren, indem wir einen Bob gegen eine Alice antreten lassen, nur, daß Bob zum Start 50 Millionen Euro und 500.000 Aktien bekommt.
In der Realität heißen die Super-Bobs zum Beispiel Blackrock, es sind Aktienfonds, Hedgefonds, Big Player, die das Kapital vieler anderer verwalten.
Doch unsere kleinen Bobs sparen nicht gern in solchen Fonds, da die Gewinne nur gering ausfallen. In unserem Beispiel könnten die 5000 Bobs zum Super-Bob vereint der Alice genau eine Million Euro abknöpfen, die sich die Bobs dann untereinander aufteilen müßten - für jeden sind das gerade mal 200 Euro.
Drum kämpfen alle Bobs für sich sich selbst mit kleinem Kapital, in der Hoffnung, den Big Boys die Kohle abzunehmen, dabei ist es meist umgekehrt.
Wenn die Bobs richtig viele werden, wenn etwa 15.000 Bobs oder mehr gegen eine Alice antreten, gewinnt Alice nicht mehr, auch, wenn die Bobs sich nicht absprechen, als Super-Bob zu agieren. Die Order-Dichte der Bobs ist dann so hoch, daß es immer genügend Bobs gibt, die sich wie ein Super-Bob verhalten - es entstehen Zufalls-Super-Bobs - so wie im realen Leben hin und wieder ein paar durchgeknallte Wallstreet Bets sich über Foren verabreden und als Super-Bob auftreten.
Der Chart von 15.000 Bobs gegen eine Alice ist langweilig. Es geht ewig seitwärts - keine Kurskapriolen, keiner schafft es Reichtum anzuhäufen.
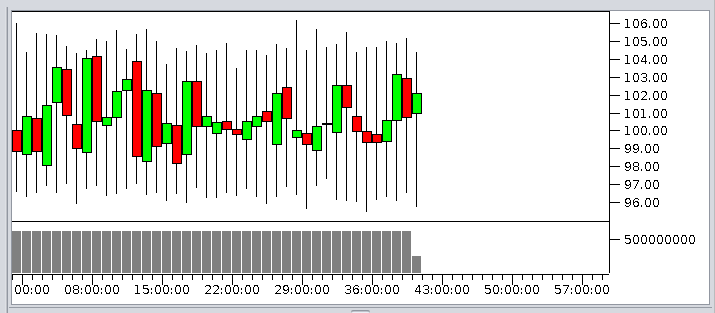
Und Alice hat auf fast wundersame Weise ihre Million verloren, sie ist aber auch nicht ruiniert, sie wird nur so arm wie die Bobs arm sind, sie wird zu einem durchschnittlichen Bob. Im Ranking ist sie aber dennoch auf dem letzten Platz, da sie den größten prozentualen Verlust hat.
Für das Trading hilft dir diese Erkenntnis aber auch nicht weiter.
Was du mitnehmen kannst: Es ist sehr wahrscheinlich, daß du beim Trading den Gamblers Ruin erleidest. Alice' Strategie ist saudumm, die Strategien der Bobs sind ebenso saudumm, und dennoch gewinnt (fast) immer Alice - einfach nur, weil sie mehr Geld hat.
Ja aber, wirst du jetzt vielleicht denken, du wirst doch nicht so eine saudumme Strategie fahren wie die Bobs und Alice.
Aber das machen die anderen in der realen Welt auch nicht. Jeder hat seine Strategie, eine schlaue, die schlauste, auch Alice, doch in der Summe sind alle Strategien wie Zufall, das sagt die Hypothese der effizienten Märkte. Und selbst unter den Bobs, die saudumm per Zufall ihre Orders plazieren, ist irgendwann einer dabei, der das Glück hat, als Gewinner hervorzugehen.
Probier es aus! Wirf Alice raus und laß 2 Bobs gegeneinander antreten. Einer wird gewinnen, einer geht pleite. Es gewinnt der, der mehr Glück hatte. Probier es mit 10 Bobs. Einer gewinnt, 9 gehen pleite. Nimm 100 Bobs! Einer gewinnt per Zufall, der Rest geht pleite. Aber ab 500 Bobs gewinnt keiner mehr. Die Wahrscheinlichkeit, daß es zu der "glücklichen" Strategie eines einzelnen Bobs nicht einen gibt, der eine Gegenstrategie hat, wird immer geringer.
Wenn du als kleiner Fisch gegen die Big Boys in effizienten Märkten antrittst, gewinnst du allerhöchstens dadurch, daß du Glück hast - nicht aufgrund einer genialen, gebacktesteten Strategie. Und beachte, daß wir hier in unseren kleinen Simulationen den klassischen Aktienhandel betrachtet haben - ohne Transaktionskosten, ohne Hebel, ohne Margin, ohne Zinsen - und schon da haben die Kleinen keine Chance.
Zum Abschluß noch ein Bild des Programms im CDE/Motif-Look-and-Feel. Ist das nicht schön?
Schreib einen Kommentar